重拾诚信
| Civic honesty around the globe | 各国市民的诚实度 |
| Alain Cohn, Michel André Maréchal, David Tannenbaum, Christian Lukas Zünd | 阿兰∙科恩,米歇尔-安德烈∙马雷哈尔,大卫∙坦南鲍姆,克里斯琴-卢卡斯∙津德 |
| Science Journal / July 5, 2019 | 科学期刊 / 2019年7月5日 |
Abstract / 摘要
国民的诚实对于社会资本和经济发展至关重要,但时常与自身的物质利益相冲突。我们通过在全球40个国家的355个城市进行实地测试,来检视诚实与私利之间的平衡。在这些实验中,我们在公共场合和私密机构放置了17,000多个装有不同金额的钱包,看捡到钱包者是否联系失主并归还。在几乎所有的国家,对于装钱更多的钱包,人们更有可能归还。经济学家和非专业人士都未能预测到这一结果。另外的数据表明,我们的主要发现可以归因于人们的无私理念及嫌恶自己被当作小偷,两条理由都随着测试金额的增大而更显著。
诚实的行为是经济和社会生活的核心特征(1, 2)。没有诚实,承诺就不会践行,合同就不会遵守,各项税金就会被欠缴,政府部门就会变得腐败。这些不诚实的行为会给个体、机构、和全社会带来高昂的代价。例如,美国每年因逃税造成的损失估计为数千亿美元(3),发展中国家的腐败和其它非法资金流动的成本估计每年高达1.3万亿美元——大致相当于澳大利亚的国内生产总值(4, 5)。
在这份报告中,我们检视人们的诚实举动——自觉抵制机会主义行为——如何受金钱的影响而表现不同。虽然有很多文献(6–11)记述引发诚实行为的前提条件,但是鲜有提及物质刺激如何影响国民的诚信,特别是在现实环境中。明白国民的诚实与物质激励之间的关系不仅具有现实意义,而且在理论上也很重要。
各种诚信理论对物质激励的作用作出的预测各不相同。古典经济模型基于个体自身利益的理性考量,认为在其它条件相同的情况下,随着物质激励的增大,诚实行为将变得更少见(12)。融合利他主义或其它相关偏好的人类行为模型也预测,不诚实的行为会随着激励的增加而相应地上升,因为自身利益几乎总是胜过对他人福祉的关注——我们关心他人,但赶不上关心我们自己(13–15)。因此,随着可能激发不诚实行为的物质激励的增大,自身利益考量将在行为中发挥越来越突出的作用。心理学模型从维护自我形象的视角出发,预测人们会因为利益而欺瞒哄骗,只要其行为不伤及他们的自我概念(7, 16)。但是事先并不清楚,随着物质激励的增大,自我形象问题是否会变得更(不)重要,两者之间的关系将如何此消彼长。更棘手的是,大多数关于诚实行为的试验性文献只涉及少许的财务利益,在实验室环境中进行(受试者知道有人在观察他们的行为),并且受试者主要是西方人,受过教育,来自工业化、富足的民主社会(17)。
我们在全球范围内进行了一系列大规模的实地试验,以检视财务刺激如何影响国民的诚信。我们放置了“丢失”的钱包,其中装有用于实验的不同数额的钱币,让我们能够在广泛的社会和机构样本中确定,财务利益如何影响钱包的归还率。我们的实验从经典的“丢失的信件”研究中获得灵感,该项研究检视在自然环境中的行为,这次试验比过去的研究受到更严格的控制(18, 19)。
我们造访了40个国家的355座城市,总共放置了17,303个钱包。我们通常在一个国家中选取5–8座最大的城市,每个国家大约有400个观测值。钱包被放置在5类社会机构之一:(i)银行(ii)影剧院、博物馆、或其它文化场所(iii)邮局(iv)酒店(v)警察局、法院、或其它公职场所。这些机构可以作为有用的基准,因为它们在各国都很常见,并且通常有一片公共接待区域,我们可以在那里掉落钱包。
我们的钱包是透明的名片盒样式,这样捡到钱包的人不必打开它就可以看到其中的内容物。我们设置的关键独立变量是钱包内是否装钱,我们随机地放置没有装钱或装有$13.45美元(分别记录为“无钱”和“有钱”状态)的钱包。我们采用当地的货币,为确保国家之间的可比性,根据各国的购买力调整了放入钱包的金额。每个钱包内还放有3张相同的名片、一份购物清单、和一把钥匙。名片上有丢失钱包者的姓名和电子邮箱,我们在每个国家使用的都是虚构但常见的男性名。购物清单和名片都是用该国的本土文字印制,以显示丢失钱包者是当地居民。
进入大楼后,我们的一名研究助理(研究助理共有11名男性和2名女性)走近柜台的一名员工说:“嗨,我在街道的拐角处发现了这个[指着钱包]。” 然后把钱包放在柜台上,推到员工面前说:“有人丢失了这个钱包。我赶时间,得马上走。你可以处理一下吗?” 研究助理说完就走出了大楼,没有留下联系方式,也没有索取交付钱包的书面证明。我们衡量结果的主要标准是接收者是否联系了钱包主人以便退还。我们为每个钱包创建了单独的电子邮件地址,记录了钱包掉落后100天内收到的电子邮件。完整的方法和结果,包括额外的稳健性检查,比如测试实验效果,请参见补充材料。
如下图的左侧面板所示,我们的全球实验返回了非常一致的结果:人们更有可能报告其中装有钱的钱包,而不是没有装钱的掉落钱包。我们在38个国家(总共40个国家)中观察到了这种模式,对于其中装有钱的钱包,我们没有发现任何国家的报告率有统计上的显著下降。放钱到钱包中会增加报告的可能性,平均而言,从“无钱”状态的40%上升到“有钱”状态的51%(P<0.0001)。限定接收者和情境特征该结果也成立。此外,虽然国民的诚实比率因国家而异,但各种条件下诚实比率的绝对增加值保持稳定。如下图的右侧面板所示,基于绝对报告率的平均处理效应在四分位数上大致相等。
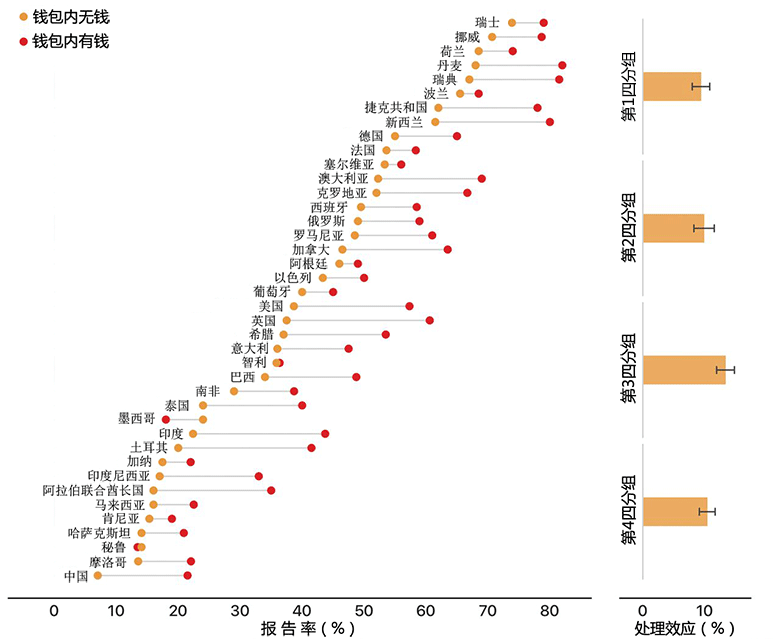
钱包装有钱时,人们表现出更大的诚实性,但可能是因为金额不够大,财务上并无意义。为检视这种可能性,我们还在3个国家(美国、英国、波兰)进行了“大额”测试,将装进钱包的金额增大到$94.15美元,初始金额的7倍。结果显示,当钱包装有相当数量的钱时,所有3个国家的报告率都进一步提高。汇总3个国家的报告率从“无钱”状态的46%上升到“有钱”状态的61%,在“大额”条件下达到72%(所有成对比较中P<0.0001)。
于是我们转向这个问题,为什么人们更有可能归还装钱更多而不是更少的钱包。我们的研究设计可以让我们排除几种可能的解释。我们首先考察的可能性是,收到钱包者担心会受到法律处罚,如果不归还钱包,特别是其中的金额更大的时候。为解答这个问题,我们仔细查看报告率是否受到这些因素的影响(i)收到钱包时旁边是否有其他人(ii)建筑物内是否安装有摄像头(iii)美国各州针对丢失财物的法律有何不同。如果收到钱包者担心可能的惩罚或可能被察觉,那么诚实度应该伴随这些变量而增大,但我们发现这些因素都不能够解释不同条件下报告率的明显变化。第2种解释是我们只记录了收到钱包者是否归还了掉落的钱包,对于装有钱的钱包,收到钱包者还可能退还了钱包但截留了其中的现金。我们审核了部分归还的钱包,没有找到支持相关解释的证据:我们收到的钱包中超过98%的钱被退还回来。第3种可能的解释是,在退还装钱较多的钱包时,收到钱包者期望得到更多的酬谢费。在美国、英国、和波兰进行的全国抽样调查中,我们询问受访者,就我们放入钱包中的金额而言,在退还钱包时希望得到多少酬谢。我们未能找到证据来说明,人们在归还装钱较多的钱包时期望得到更多的酬谢。
排除了这3种可能的解释之后,我们接下来制定并测试一个简单的行为模型,该模型概括表达数据结果中观察到的模式(完整的模型细节可参见补充材料)。在我们的框架中,决定诚实度的是4个组成部分之间的相互作用:(i)保留钱包的经济回报(ii)联系掉落钱包者的固定努力成本(iii)对掉落钱包者的无私关心(iv)与被看作小偷这种负面形象相关的成本(我们称之为偷窃厌恶)。
我们框架中的一个关键点是,关心他人的影响因素包括钱物对于掉落钱包者的价值,而偷窃厌恶的影响因素只包括钱物对于收到钱包者的价值。为了区分这两种动机,我们在美国、英国、和波兰各地进行了“有钱-无钥匙”测试,钱包中装有与先前测试同等金额的钱但没有钥匙。跟钱不同,钥匙对于掉落钱包者有价值但对于收到钱包者没有价值,因此“有钱-有钥匙”和“有钱-无钥匙”测试之间的任何差异都可归因于对他人的关心。结果显示,相对于没有钥匙的钱包,报告装有钥匙的钱包的可能性平均高出9.2个百分点(汇总各国结果P=0.0001)。这表明收到钱包者报告归还的部分原因是,他们担心不归还会对掉落钱包者造成的麻烦。
我们框架中的第2部分——对于解释装钱更多的钱包归还率更高的结果十分重要——涉及厌恶把自己看作小偷。在美国、英国、和波兰进行的全国抽样调查中,我们让受访者想象,收到4种状态(无钱、有钱、多钱、有钱无钥匙)之一的钱包,如果没有退还,他们会在从0(完全不是)到10(强烈认可)的何种程度上感觉自己像是小偷。受访者表示,如果没有退还装有钱的钱包,那么会觉得更像是偷窃,当钱包内装有很多钱时,这种感觉会更强烈(全部成对比较结果P≤0.007)。这告诉我们,不退回钱包的自我感觉成本可能会随着金额的增大而上升,这与实际报告率的行为数据一致。相比之下,我们在比较有无钥匙、装有相等金额的钱包时,却没有观察到“偷窃感觉”在数值上的明显差异(“有钱”与“有钱无钥匙”相比较P=0.259)。这告诉我们,厌恶偷窃的感觉可能跟对于收到钱包者有价值的内容物相关,例如钱包内的现金,而跟对于掉落钱包者有价值的内容物无关。尽管调查得来的回答并不完全代表真实的行为,应该小心诠释,但这些发现与此假设一致:不诚实行为的财务结果还与心理成本有关,心理成本的增大会超过不诚实行为的边际收益。
在最后一组研究中,我们考查人们是否预计到诚实度的这种结果。我们让299名参与者预测,对于装有$0美元、$13.45美元、和$94.15美元的钱包(对应于我们的“无钱”、“有钱”、和“多钱”状态),美国人的归还率会有多大。为鼓励准确性,我们告知参与者,最准确的预测将获得现金奖励。结果显示,参与者的看法与行为数据大相径庭。参与者预测,钱包中没有装钱时,诚实度会最高(预估的报告率中值M=73%,标准差SD=29),钱包中装有少量的钱时,报告率会降低(M=65%,SD=24),钱包中装有更多钱时,报告率会进一步降低(M=55%,SD=29)。预估的不同状态下的报告率变化均值与实际变化值出入很大(全部成对比较结果P<0.001)。当钱包内的金额增大时,64%的参与者错误地估计报告率将会下降,18%的参与者正确地估计报告率将会上升(符号检验结果P<0.001)。另外的询问表明,参与者的估计反映出了人类行为的心理模型,夸大了狭隘的自身利益的作用(20, 21)。当钱包内装有更多钱时,参与者估计自身利益的作用会增大,对掉落钱包者的无私关心会消减,至于偷窃厌恶对报告率的影响,参与者几乎没有给予重视。
普通公众错误地估计了人们将如何回应钱包价值增大的情况,也许专业的经济学家会估计得更准确。我们请279位学术表现领先的经济学家对此作预测。跟非专业人士一样,他们也未能预计到,报告率会随着钱币金额的增大而上升。受访者普遍预测,国民的诚实度在钱包内“无钱”和“有钱”状态下(数值分别为 M=69%,SD=25 和 M=69%,SD=21)将高于“多钱”状态(M=66%,SD=23)。这些预测与我们在各种条件下观察到的实际变化也是显著不同(全部成对比较结果P<0.001)。不过经济学家的校准误差不像我们的非专业人士那样严重。当钱包内的金额增大时,49%的经济学家错误地预测报告率将会下降,29%的受访者正确地预测报告率将会上升(符号检验结果P<0.001)。
我们在40个国家进行了实地操作,测试人们面对更强的经济诱因时,是否会更不诚实地做事情,我们发现实际情况正相反。人们更可能归还装有较多钱币的钱包。这一结果在各个国家和机构中都表现得很明显,即使在诱发不诚实行为的经济诱因很大时也是如此。我们得到的结果与融合利他主义和自我形象关注的理论模型相一致,同时也表明理论应该作修改,即非金钱动机直接与不诚实收益相互作用。当人们可以从不诚实的行为中获得较大的利益时,作弊的欲望会增强,但同时把自己看作小偷的心理成本也会增大——有时候后者会胜过前者。
我们得到的结果也提供了一组独特的数据集合,用来检视各国民众的诚信差异。诚实是社会资本的一项重要组成部分(22),这里我们提供了一套客观的衡量标准,以补充传统上采用主观调查来检验社会资本的大量工作((2, 23–25)。查看各国的平均报告率,我们发现国民的诚信度差异很大,从14%到76%不等。即使设定国内生产总值的区间,这种差异也明显存在,表明除财富之外的其它因素也在发挥作用。在补充材料中,我们给出的分析表明,经济上有利的地理条件、包容性的政治制度、国民的受教育程度、文化价值观重视超越小团体的道德规范,都与国民的诚实度正相关。需要进一步的研究来确定这些因素和其它因素是如何造就诚实行为的社会差异。
Above contents are translated from / 以上内容译自
https://science.sciencemag.org/content/early/2019/06/19/science.aau8712
